細かい議論
日射量と、パネル角度と、発電量と、の関係について考察してみました。
１．水平配置と切妻対称配置
他でも書いたように。我が家の屋根は東西向きの傾斜約２４°の切妻屋根です。正確には、東面が少し北に、西面が少し南に振っていますが、東北東・西南西までは向いていません。この２面による合計発電量が全天日射量とほぼ比例する、と見ているのですが、その妥当性を考察します。
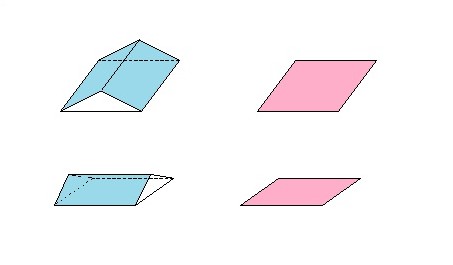
話を単純にするため、切妻屋根全面にパネルが載っているものとしましょう。そして、比較対象として、水平配置のパネルを考えてみます。水平パネル(図のピンク色）の形は、切妻パネル２枚（図の水色）を水平面に投影した形であるものとします。真上から見て、切妻パネルと水平パネルとを同じ形同じ面積にするわけです。これは真上からの光に対する発電量を、切妻パネルと水平パネルとで同じにすることになります。パネル面積としては、切妻パネルの方が斜めになっている分広いことになります。
この切妻パネルと水平パネル(図のピンク色）とを斜めから見てみます。上図のように、切妻の両面が見える方向からの、パネルの見かけの面積が水平パネルの見かけの面積と同じなのがお分かりいただけるでしょうか。水色形状から、切妻側面の三角形を引いて足したらピンクと同じ平行四辺形になります。このことは、視線方向からの光に対する発電量も、切妻パネルと水平パネルとで同じになることを意味します。
下図のように、切妻の一方の面が見えない向きから見ると、水色の方が大きく見えます。（見えていない面積をマイナスとみなすと同じ面積になりますが、太陽光パネルなのですから、光が当たらない状態でも０以下にはなりません。）
この方向からの光に対しては、光の向きに立っている面が稼ぐ分、切妻パネルの方が発電量が多くなります。切妻パネルの方が元々面積が広いのですから、自慢できることではありませんが。
２．気象台発表の全天日射量と発電量の相関
実際に実用に供されることはまず無いと思いますが、水平面配置のパネルなら、全天日射量と最も強い相関が期待できます。パネルの温度特性のような、パネル変換効率自体の変動以外では、気象台とパネルの位置の違いで雲の状態が違うことだけが相関を乱す要因となります。
それに準じて強い相関が期待できるのが、切妻対称配置になります。実用的には東西面に近い配置になるでしょう。１．のように、屋根傾斜より高い角度の光線に対しては水平配置と同一で、差が出るのが低い角度の光線に対する分だけになります。屋根傾斜が小さめなら、ますます差が出にくくなります。
東面だけ、あるいは西面だけ、というのは、期待効率は切妻対称配置と同じになりますが、全天日射量との相関は少し悪くなります。東面だけのパネルは、朝晴れて夕方曇る日には稼ぎますし、夕方から晴れる日には稼げなくなります。このような一日の中の日射量変動が、全天日射量との発電量との相関を悪くしますが、季節変動分は温度の影響以外は現れないはずなので、水平面配置、切妻対称配置に対して、相関だけが少し悪い、という感じになると思われます。言い方を変えると、ここまでのケースでは、全天日射量と発電量との間に(温度の影響はあるものの）通年で共通の回帰式が期待できることになります。
最も理想的とされ、実施例も多い南面配置は、色々ややこしいことになります。全天日射量が太陽が高ければ大きくなるに対し、南面での発電量は傾斜の正面に太陽が来たときに一番大きくなります。明らかに通年で共通の回帰式は使えません。ちゃんと計算するには、色々なところが提供しているシミュレーション相当の計算をすることになるはずで、かなり敷居は高くなります。それでも、月ごとの実績でしか比較できないソーラークリニックのシミュレーションだけ見ているよりは、日々の全天日射量との相関を見るほうが早く確実に異常に気づくことが出来るはずです。通年で共通の回帰式は使えませんが、月単位での集計には回帰式を当てはめることができ、前年同月との比較が出来るようになります。一ヶ月合計発電量という一つだけの数字をシミュレーション結果と比べて少ないような気がする・・・というのに対し、３０日間の毎日のデータ合計３０個を日射量と付き合わせれば、正常／異常の判断が確実に出来るはずです。
＃日々の発電量が多かった少なかったと一喜一憂するより、「今日も日射量に対して妥当な発電量だった」と泰然としている方が、精神衛生上よろしいように思いますし。
３．東西面パネルの効率
１．では結局のところ、「東西面のパネルの発電能力は、水平面に投影した面積のパネルの発電能力に近い」という意味のことを言っているのですが、もう少しちゃんと検討してみます。例えば、東面で屋根傾斜９０°
（という言い方は普通しなくて、つまりこれは東向いた壁そのもの）にパネルを張ると、水平面への投影面積は０ですから、１．の流儀では発電能力も０になるはず・・ですが、実際には朝日を壁一面に受けて結構発電するはずです。１．では無視することにした、「低い角度の光線での効率上昇」が、無視できるどころかそれが全てになってしまっているわけです。
（ちなみに、１．では、水平パネルの効率を１とした時の、
傾斜角αのパネルの効率を cosα とみなしていたことになります。）
ではどうするか。シミュレーションでのちゃんとした計算をするのでなければ、計算を始めるのに何かの仮定をおく必要があります。例えば、「低い角度から来る光の量も、高い角度から来る光の量もみな同じ」というのはどうでしょうか。これは、北−天頂−南 の円弧に当てはめるとしたらナンセンスです。北も南も水平線上に太陽が来ることはないのですから。しかし、東−天頂−西 の円弧なら、まあまあ悪くないような気もします。赤道上であるならごく正当な仮定と思われます。これでやってみましょう。
水平面パネルは日の出から日の入りまで光が当たります。
瞬時の発電量は太陽の高さをθとして、ｓｉｎθに比例します。
ピーク出力を A として一日分通算すると、∫A
sinθ＝ 2A (積分範囲は０からπ） となります。
西向きで屋根傾斜αのパネルを考えます。
日の出からしばらくは影に入っていますが、日の入りぎりぎりまで光が当たります。
一日分の通算は、∫A sinθ＝ （１＋cosα）A (積分範囲はαからπ）
従って、水平パネルの効率を１とすると、傾斜角αのパネルの効率は、
（１＋cosα）／２ となります。
この計算結果をソーラークリニックのシミュレーションと比較してみましょう。この頁の最後のグラフを無断借用して、計算結果を強引に重ね書きすると・・・
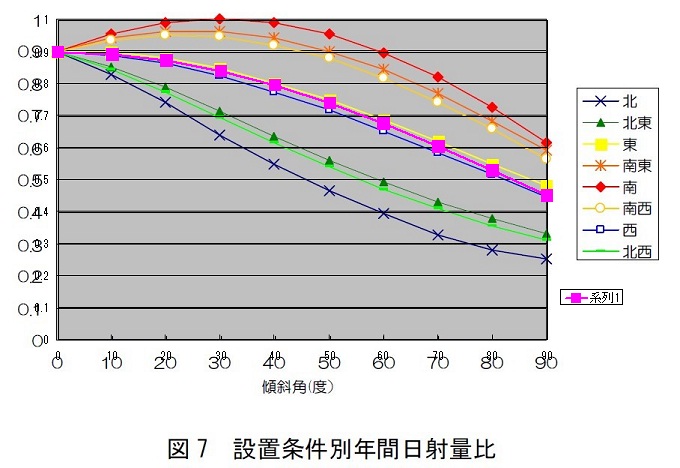
ピンクで書いた「系列１」が見事に「東」と「西」の間に入りました。
ソーラークリニックのシミュレーションで、東の効率が西よりよいのは、午前中の気温が上がる前に発電できるのを考慮したものと思われますが、ともかく、そこまで色々考えて引いたであろう２本の線の間に、今回の野蛮な前提の線が入ってくるのですから、野蛮な前提は結構妥当だったと考えられます。
こちらの頁の最後で検討した総合効率の計算で、「傾斜の影響による受光効率９５．６％」としましたが、これは屋根傾斜２４°に対して、（１＋cos２４°）／２ ＝
０．９５６ という計算結果を用いています。
４．アメダスの日照時間データによる全天日射量データの補正
別のところでも書いたように、全天日射量は名古屋地方気象台のデータしか得られませんが、同気象台は自宅からは約２０ｋｍの距離があります。近隣のアメダスには東海（約１０ｋｍ）、岡崎（約２０ｋｍ）とあったのですが、何と、東海のアメダスが１０月１７日で撤去されて、替わりに大府（約５ｋｍ）に配置換えになりました。それはともかく、この近隣アメダスの日照時間データをどうにかして活用できないか、検討を重ねてきた成果を、ついにお披露目することにしました。
こちらが、２０１２年１０月までの名古屋の日射量と発電量をプロットしたデータ、
紺色が6月、ピンクが7月、黄色が8月、水色が9月、紫が10月です↓
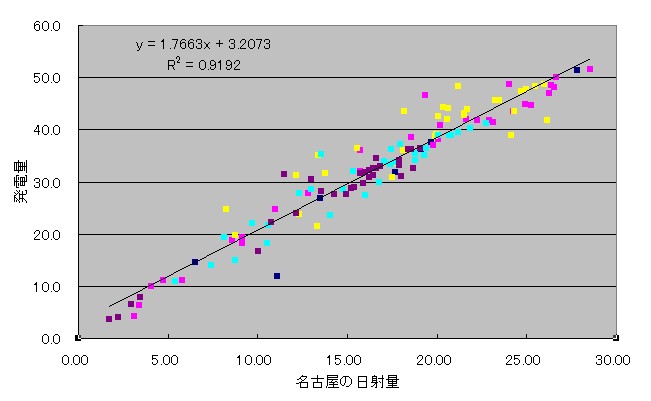
こちら↓が、「名古屋と岡崎の日照時間を使って補正した日々の日射量」と発電量をプロットしたデータ。
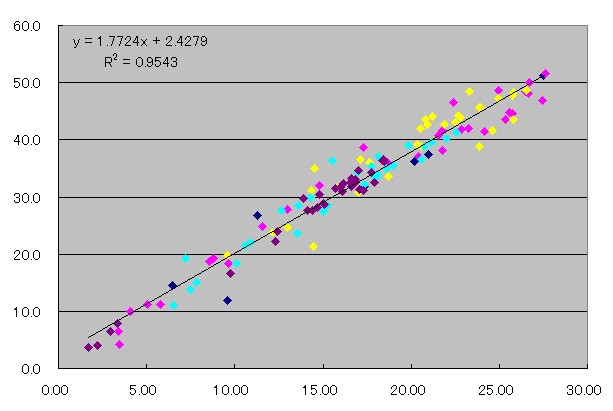
元のグラフでも中々のものですが、こちらは一段と凄い相関を示しています。
名古屋の日々のデータとして、日射量と共に日照時間も出ています。岡崎は日照時間だけがあります。この日照時間の違いを反映させる方法を考えたわけです。実際にはもっともっと色々試しましたが、本線だけ以下に説明します。
まずは、日々の日射量を、名古屋の日射量×（岡崎の日照時間／名古屋の日照時間） という式で補正するのはどうでしょう。名古屋の日照時間が10時間、岡崎の日照時間が11時間だとしたら、日射量を10%増しにする、という考えです。10時間とか日がしっかり照っている場合には結構良さそうですが、曇りとか雨だと、日照時間が０時間ということもあります。名古屋の日照時間が0時間だと、この式の分母に０が来てしまうので使えません。
それで、実際に最初に検討したのは、名古屋の日射量×（岡崎の日照時間＋α）／（名古屋の日照時間＋α） という定数αを導入した式です。このαを加減して、相関係数
R2 が最大になるようにする、というのを考えました。しかしこれだと、日照時間が短い／日射量が少ない場合に補正がかかりにくい、という特性があります。
そこで、日照時間／日射量に応じた補正がかかるようにと、日々の日射量の補正式として、
名古屋の日射量×（岡崎の日照時間＋β×名古屋の日射量）／（名古屋の日照時間＋β×名古屋の日射量）
という式を最終的に採用しました・・・・もはや物理的意味は説明しようもありませんが。
今のところ、このβを１とすると R2
が最大になるので、それで描いたのが上のグラフになります。
ばらつきの大きかった8月（黄色）もぐっと近似線に接近しています。その他で分かりやすいのは10月（紫）でしょうか。補正なしでも相関係数は大きいのですが、発電量２０kWh以下のデータを除外してしまうと、相関がはっきりしなくなります。それが補正後だと、発電量２０kWh以上のところだけみても、はっきりと右上がりの相関が見えるようになります。なお各月単月の相関係数は
７月 ：0.9588 → 0.9706
８月 ：0.787 → 0.8651
９月 ：0.9091 → 0.9392
10月：0.9392 → 0.9842
と、当然とはいえ、どの月も上昇すると共に、単月の近似線（上図では描いていませんが）が、8月を除いて殆ど重なってきます。8月はやはり格別好調だったようです。
東海／大府の日照時間に対しても同様のやり方を試みましたが、岡崎の場合ほど高い相関係数が得られませんでした。控えめに言っても、夏から秋にかけての刈谷の雲のかかり方は東海よりは岡崎に近い、とは言えそうです。冬から春にかけての雲の流れ方が違ってくる、という可能性もありますし、今後、大府のデータが増えていくと、何と言っても距離が近いですから、こちらを採用すべし、ということになるかもしれません。
ともかく、夏至の頃から秋分を大分過ぎるまでのデータを重ねて、この相関係数です。東西切妻両面の発電量は全天日射量に相関するはず、という予想を一段と強く裏付けるものですし、発電効率の温度依存は極めて低そう、という推定も可能になります。
（パネル劣化と温度依存が相殺している、という可能性は、もう一度気温が上がるまで否定できませんが）
５．アメダスの日照時間データによる全天日射量データの補正（その２）
上の節で書いたように、東海にあったアメダスが大府に配置換えになって随分日が経ちました。東海／大府の日射量も毎日記録していたのですが、ものは試しと、アメダス配置換え以降の、名古屋の日射量と、名古屋／大府／岡崎の日照時間と、を使って相関係数の改善を試みてみました。
こちらが、２０１２年１０月１７日からの名古屋のデータを補正した日射量と発電量をプロットしたデータ、
ピンクが2012年（１０月7日〜）、黄色が2013年（〜５月３１日）月です↓
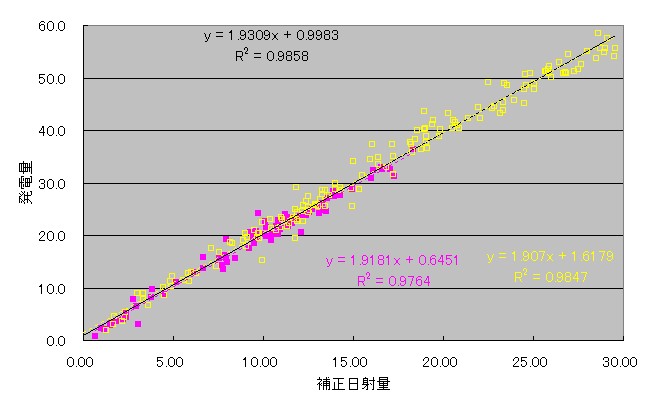
黒の数字が通算での相関係数ですが、とにかくどれを取っても凄い相関係数になっています。
従来は、日々の日射量の補正式として、
名古屋の日射量×（岡崎の日照時間＋β×名古屋の日射量）／（名古屋の日照時間＋β×名古屋の日射量）
という式を採用して、そのβを１としていたのですが、今回は
名古屋の日射量×（岡崎の日照時間＋β×名古屋の日射量）／（名古屋の日照時間＋β×名古屋の日射量）
×（大府の日照時間＋γ×名古屋の日射量）／（名古屋の日照時間＋γ×名古屋の日射量）
と、双方の日照時間を考慮できるようにした上で、
R2 が最大になるようにβとγを調整しました。単年と通算で最適値が若干違いますが、β＝２．５、γ＝０．８ で統一しています。β＞γというのは、大府の日射量の影響をより強く受ける補正であることを意味します。
これでやると、
・２０１２年、２０１３年、通算、どの見方でも相関が極めてよくなります。
・２０１２年と２０１３年とで、成績の違いは殆どありません。
（補正無し、あるいは岡崎だけで補正すると、２０１３年の方が２０１２年より好成績ということになります）
２０１２年の６月２４日から１０月１６日までは、大府の日射量のデータがないのですが、これを東海のデータで置き換えると、２０１２年通しの相関係数は
R2 ＝0.9652 と岡崎だけの補正よりも悪くなるのですが、近似線は１０月１７日以降だけのものと殆ど変わりません。
というわけで、今後の比較のベースとする「２０１２年後半補正付き」の日射量は、東海／大府と岡崎、両方の日照時間を、東海／大府のデータをより重視する形で補正したもの、とします。
太陽光TOPへ TOPへ