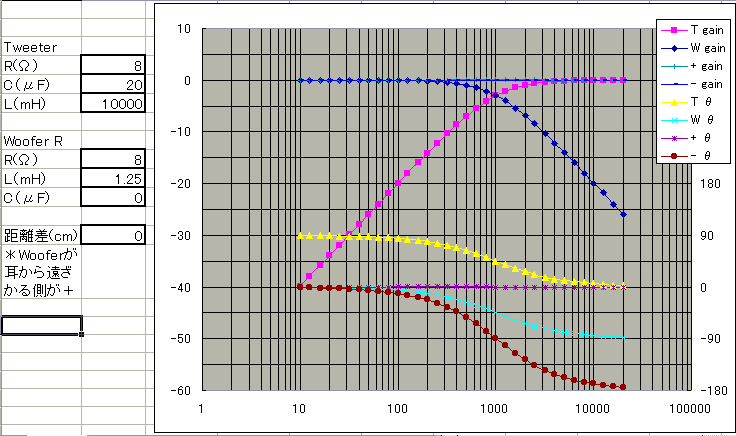
8Ωのユニットで1kHzクロスの例です。総合ゲインの線は正相(+gain)も逆相(-gain)も一直線、完全に重なっています。位相特性では、正相(+θ)が一直線、逆相は高域に向かって180度回転します(だから逆相)。
ネットワークの常識非常識
長岡先生の勘違いを僭越ながら指摘するページになります。ただし、先生にだまされたことにはなりません。何れも先生が、「理論上こうだが、実際のスピーカーではやって見るまで分からない」としていたポイントです。その理論のところで勘違いがあっただけで、スピーカー工作普及における先生の功績にいささかも傷がつくものではありません
その1:同じスピーカーの並列接続では、理論上音圧+6dB、直列接続では±0dBになる。
長岡先生の本では、同じスピーカーユニットを2本使う場合、並列接続で1本使用に対して+3dB、直列接続で同じく−3dB、となっています。一方、私がスピーカー測定を始めるきっかけとなった誠文堂新光社刊、オーディオクラフトマガジン2の「スピーカシステムQ&A」(佐伯多門氏執筆)では並列では「最大6dB増加します」、とあります。
これは「最大」+6dBが正しい。佐伯氏はプロのスピーカー屋としてあくまで正しいことを書いているのですが、素人に分かる文章ではありません。そこをなんとか、と思うのですが、実は私も本業で騒音測定とかに首を突っ込んだことがあって、真っ白の素人とはいいがたいので、うまく説明できるかどうか。また長岡先生が全く間違いともいえないのです。
まず、音圧のdB表示ですが、http://www.jvc-victor.co.jp/pro/sound/nani/talk-4.html
より、
SPL=20log(P1/P0)、ただし、
SPL:音圧レベル、Sound
Pressure Levelの略
P1:その音の音圧
P0:基準音圧=2×10-5(Pa)
です。音「圧」(=圧力振幅)が倍になると6dB増える(その時の「音のエネルギ」は4倍増)、「音のエネルギが倍」なら3dB増、という表示です。
定電圧駆動のアンプが前提ですと、並列と直列とを比べると、投入エネルギーが4倍違ってきます。話を簡単にするため、8Ωのスピーカーユニットでアンプ出力電圧が8Vとしましょう。スピーカーユニット1本なら、電流1Aです。2本並列なら各ユニットに1A、2本直列なら各ユニットに0.5Aです。ユニット電流が倍=ユニット端子間電圧が倍=音圧が倍、と言ってもいいですし、投入電力(=電圧×電流)が4倍=音のエネルギが4倍、と言ってもいい、とにかく「6dB違い」です。2つのユニットが同一の動作をするという点では直列でも並列でも同じですから、後述する1本と2本の比較のような込み入った話にはならず、電圧が倍⇔電力が4倍⇔音は6dB違い、と決め付けても構わないのです。
さて、次は1本と2本の比較です。結構ややこしい話になります。
「長岡鉄男のオリジナルスピーカー設計術2 こんなスピーカー見たことない(図面集)」をお持ちの方はD−37とD−66とを比較してみてください。同じユニットの1本と2本並列、ほぼ同じ音道設計で幅だけが倍半分、の2つのスピーカーですが、ほぼ全域に渡り3dBというより6dBの差がついています。ライブではあっても広い広い箱舟での測定ですから、こうなるのです。。。
2個並列で、投入エネルギーが2倍、であれば音のエネルギーも2倍だから、音圧は+3dB、と思う方が素直なのです。投入エネルギーが2倍なのに音圧が4倍になるはずがない!・・かどうか。実は「最大」ならそうなるのです。おかしくないのか?おかしくないのです。
まず、並列の極端な例として、モノラルの信号をステレオの2本のスピーカーで聞こうとしている状態をイメージしてください。長岡先生の著作に忠実な貴方は、切り株に腰掛けないまでも、二本のスピーカーから等距離の位置、二等辺三角形の頂点に座っています。貴方はまず左のスピーカーだけ鳴らします。±P(Pa)の圧力変化すなわち音波が耳に届きました。貴方は次に左右のスピーカーを同時に鳴らします。1+1=2、すなわち圧力変化は±2P(Pa)です。音のエネルギーとしては2の自乗、すなわち4倍、6dBの増加になります。
・・・・・だまされた気になるほうが正常だと思います。ポイントは、二等辺三角形の頂点にちゃんと座った貴方にあります。左右のスピーカーから等距離ですから、波長の長い短いによらず、左右のスピーカーから発された音の位相はいつも揃っています。これがオフセンターで聴くとどうなるか。意識的に二等辺三角形の頂点に座るのでなければ、左右のスピーカーからの距離差が50cmできてしまうことは珍しくないと思います。この位置で680Hzの音を聞くとどうなるか。口笛で吹くのに具合いいくらいの結構高い音ですが、波長がちょうど50cmになりますので、位相が360度ずれて、やはり4倍=+6dBになります。では340Hzならどうか? なんと、位相が正反対になるので、うまくやると元の0倍=−∞dB(!)になります。ここでは距離差を前提にしているので、近い方の音が少しでも残るのですが。
何Hzでもいい、左右のスピーカー間隔より短い波長の音であれば、干渉の結果、聴く位置によりスピーカー1本だけの時の最大4倍から最小0倍までの範囲で音圧は変化します。ここで全空間分の合計を出してしまうと、1本のときの2倍=+3dBになります。したがってエネルギー保存の法則は崩れません。左右のスピーカーから等距離でなければ、周波数によって4倍になったり0倍になったりしますが、等距離で聴いておれば周波数によらず4倍、f特は乱れません。
では、スピーカー間隔より長い波長ではどうか? 68Hzというとかなり低い音ですが、私のスピーカーでも十分鳴っています。波長は5m、スピーカー間隔が1.5mなら空間のどの位置に行っても左右の音は強め合いしかしません。全空間のエネルギーの総和は2倍を確実に超えます。今度こそエネルギー保存の法則の危機か?
ここで、佐伯氏の説くところの「両スピーカーの相互の放射インピーダンス」になるのです。そのような波長であれば、左のスピーカーによる音波が右のスピーカーに届いた時点でも殆ど位相がずれていないことになります。右スピーカーの振動板が前進しようとするとき、振動板の前の空気は左スピーカーによっても同時に圧縮されていることにあります。「手ごたえ」のある状態、「空振り」の少ない状態です。これにより振動板振幅が同じでも放射効率が上がって音圧が上がります。
エネルギー保存の法則は大丈夫か? 大丈夫です。「手ごたえ」がありますから実際には振動板の振幅は1本だけの時より抑えられます。このことはボイスコイルのインピーダンスの減少、ボイスコイル電流の増加につながり、投入エネルギーそのものも2倍以上になります。実際はスピーカーの振動板は目の前に空気があろうとなかろうと、殆ど無関係に動いていて、投入エネルギーの大半はエッジやダンパを揺らすのに使われていますので、「手ごたえ」の増加による電流増加はわずかです。1個だけでの効率を1%(こんなものです)として、投入エネルギ100に対し出力エネルギ1になりますが、2個並列の場合、投入エネルギが202に対し出力エネルギ4というイメージでいいと思います。振動板の同じ動きに対する純粋なロス(1個あたり)99は変わらず、放射効率だけがほぼ2倍という感じです。直列なら、投入エネルギ50.5出力エネルギ1、です。
実は波長が短い場合にも放射インピーダンスにまつわる現象が起こっているのですが、放射効率の上昇と下降とどちらも起こってややこしくなるので、故意に無視しました。振動板そのものよりも波長が短いような場合は、放射効率の上昇と下降が振動板上でランダムに発生して、均せば±0と見てよいでしょう。
ここまでのところで、実は壁の反射も無視しています。虚空に浮かぶスピーカー2本で話をしてしまっているわけです。反射が強い(ライブな)部屋だと、無数の仮想音源が無作為にあるような状況になり、ごっちゃごちゃになってしまい、並列での音圧増加は投入エネルギーの増加分である+3dBと見た方が良く当てはまるかもしれません。これは測定位置にも依存します。
ここまでスピーカー2本として説明しましたが、ユニット2つでも同じことです。ただしユニット間隔は例えば20cmといった短い距離になりますので、より高い周波数まで、どこで聞いても+6dB(ただし反射がなければ)の安定した領域が広がります。・・・というところで佐伯氏の文章に戻って、複数使用での指向性の話が分かりやすくなったとしたら、私の駄文が一応の成功を収めたことになります。
ここでの教訓は、2chステレオは二等辺三角形の頂点で聞きましょう、ということにつきます。わずかでもずれたらf特なんてあったものではありません。10kHzの音波の波長は3.4cmです!・・・と言われても、このレベルの精度で等距離に位置しつづけられるはずないけれど、それでも聴けてしまうのがオーディオというものではあります。
長岡先生の誤解が問題になるのは、「2つのユニットの直列接続により能率を見かけ上落し・・・」の幾つかの作品の場合でしょう。遺作のBS−112(ステレオ2000年7月号)は測定もされていないので誤解されたままです。「長岡鉄男のオリジナルスピーカー設計術2 こんなスピーカー見たことない(図面集)」をめくっていっても、BS−83、F−43、F−75、F−120がそういう狙いになっていて、測定の結果は皆そこそこフラットで結果オーライですが、設計思想としては問題あり、見かけ能率のコントロールだけが狙いならなら1本でも2本直列でも同じはずで、コストパフォーマンスを下げていました。F−91が当初配線では低音不足になった、というのも根は同じです。
その2 : 6dB/octのネットワークでは正相接続、12dB/octでは逆相接続が基本。
「長岡鉄男のオリジナルスピーカー設計術1 こんなスピーカー見たことない」では「いちおうの目安として、ウーファー、トゥイーターとも 6dB/oct の場合にはトゥイーターを逆相にする・・・ウーファー、トゥイーターとも 12dB/oct の場合は同相でよい・・・筆者もマルチウェイの位相合わせは全てスペアナを見ながら決めている・・・どちらでも良いという場合もある。」とあります。ところが、これは目安としては正反対。このことは電気屋から見たら常識過ぎるのか、ちゃんと説明した本もなかなかありません。おかげで長岡先生が誤解し続けた? とはいえ、「全てスペアナを見ながら決めている」が最終的な正解にはなります。
問題なのはフォステクスのクラフトハンドブック第1巻でも間違いが書かれていること。どうもフォステクスは本気で誤解しているようで怖い。。
6db/oct の場合は、ゲインだけいうと、つまりf特だけいうと、正相でも逆相でも同じになって、ユニットが理想的な動作をしてくれるならフラットになります。「長岡鉄男のオリジナルスピーカー設計術2 こんなスピーカー見たことない(図面集)」のF−234では両方のスペアナ結果が載せてあって、どちらもフラットになっています。なぜこうなるかというと、クロスオーバー450Hzで、一つには両方のユニットが十分理想的な動作が可能な領域でクロスしているので、一つには波長が80cmもあるので位相ずれが殆ど問題にならないから、です。
・・・ここに以前、なぜexcelでワークシートを作らないか、の言い訳を書いていたのですが、ネットワーク計算ワークシートを作ってしまいました。こちらを御覧下さい。
6dB/oct の場合
−3dB落ちの周波数とは、ウーファーのインピーダンスとコイルのインピーダンスが等しくなった所です。ウーファー両端電圧とコイル両端電圧で位相は90度違っているので(これは周波数によらずいつも成立)、ウーファー電流はアンプ電圧に対して45度違っていて、ウーファー電流はルート(1/2)=−3dB落ち、です。これを分析すると、ネットワーク無しでのコイル電流を1とした場合、位相ずれの無い成分1/2、90度ずれた成分が1/2となります。トゥイーターとコンデンサでもおなじ事情です。
ここでウーファーとトゥイーターを同相につなぐと、各々の90度ずれた成分が打ち消しあって、位相回転無しとなり、電流値の総和は1/2+1/2=1、従って総合ゲインもフラットです。1/2+1/2=1と計算してよい、というのは、本コーナーのその1そのものです。
逆相でつなぐと、各々のずれの無い成分のほうが打ち消しあい、90度ずれ成分が重なり合って、やはり1/2+1/2=1 になってしまいます。というわけで、正相でも逆相でもF特はフラットなのですが、正相なら位相回転も無い所、逆相ではクロス周波数で90度、高域では180度回ってしまいますので、せっかくだから正相にしようよ、というのが、電気屋が考える理想的 6dB/oct、です。
これをグラフにしますと・・・

8Ωのユニットで1kHzクロスの例です。総合ゲインの線は正相(+gain)も逆相(-gain)も一直線、完全に重なっています。位相特性では、正相(+θ)が一直線、逆相は高域に向かって180度回転します(だから逆相)。
ただし、いろいろ数字を入れていただければ分かりますが、正相の場合は-3dB落ち周波数をきっちり合わせないとF特(総合ゲイン)が乱れるのに対し、逆相のほうが多少ラフでもF特が乱れません。上の例のwoofer側コイルを2.5mHとすると、正相では-6dBくらいまで落ちますが、逆相は殆ど落ちません。クロスが厚い場合は逆に」正相でゲインが上がり過ぎます。逆相のほうが厳密さを要求されないので楽だ、とは言えるようです。
12dB/oct の場合
まず「長岡鉄男のオリジナルスピーカー設計術1 こんなスピーカー見たことない」では、ピークとへこみが出来て・・と説明されていますが、へこみは出来ません。正しくコイルとコンデンサを選べば、ピークもへこみもなく、なだらかに12dB/octの線に移行します。この場合、3dB落ちの周波数では、ウーファー電流はアンプ電圧に対して90度違っていて、ウーファー電流はルート(1/2)=−3dB落ち、です。ネットワーク無しでのコイル電流を1とした場合、位相ずれの無い成分が0、90度ずれた成分が1/(ルート2)となります。トゥイーターとコンデンサでもおなじ事情です。
ここでウーファーとトゥイーターを同相につなぐと、各々の90度ずれた成分が打ち消しあって、ずれの無い成分は最初から無いのですから、従って総合ゲインは0、dB表示するなら−∞です! 逆相でつなぐと、90度ずれ成分が重なり合って、1/(ルート2)+1/(ルート2)=(ルート2) になり、+3dBのピークを作ります。勿論+3の方が−∞よりまともなのは言うまでもありません。
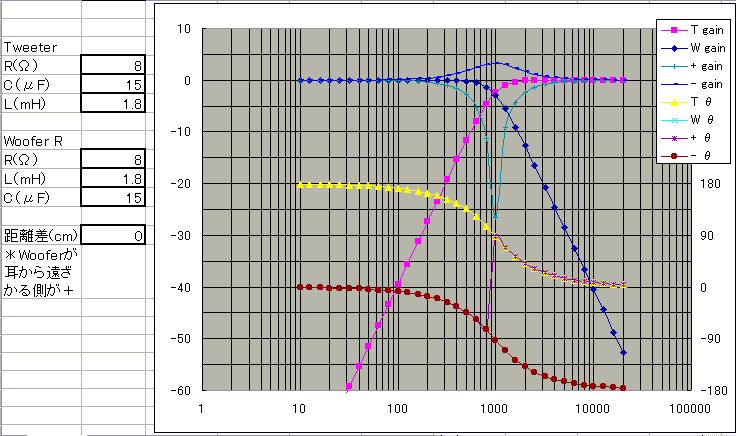
そもそも、-12dB/octで−3dBクロス、とすると、御覧の通り、ウーファーは低域での電圧電流同相から高域での電圧電流逆相へ、トゥイーターはの低域での電圧電流逆相から高域での電圧電流同相へ、どちらもなだらかに位相が変わっていくのですが、この2つの位相曲線の形がそっくりなのです。つまり逆相接続とすれば、どの周波数においてもウーファー電流とトゥイータ電流の位相が同じになるのです。これは非常に安心できることなのです。正相接続とするといつも両電流は逆相、そこで電流値が等しくなるクロス点では打ち消しあって−∞になってしまう訳です。
+3dBも嫌だ、となると、−6dBクロス、というセコイ技(フォステクスのハンドブックに説明あります)を使うことになるのですが、この場合はウーファーとトゥイーターとで、電圧と電流の位相が90度ずれになる周波数をずらすことになりますが、やはり逆相接続の方がよりフラットとなり、正相では−∞では無いにせよ、大きな凹みは出来ます。
とはいえ、実際にはこうならないことも多いわけで、長岡先生は測定の結果としてしばしば逆相を選択されています。これにはユニット自体、おそらく特にウーファーが単純な抵抗負荷ではなくて位相が狂うこと、取り付け位置による位相ずれがあること、その他もろもろの影響によるものと思われます。2kHzクロスとなると波長は17cm、これはユニットの取り付けピッチに近い数字です。リニアフェイズを目指すといっても、ボイスコイル位置で合わすのか、コーン底位置で合わすのか、はっきりせず、そのくらいのあいまいさも波長と同水準となります。
というわけで、聴いてみて測定してみておかしくなければ何でもあり、の同相/逆相論議なのですが、しかしフォステクスにはちゃんとしてもらわねば。クラフトハンドブック第1巻にかかれているグラフの正相と逆相の表示〈点線と実線)が全くの逆、それだけなら誤植かとおもえば、説明文の中でも、−3dBクロスで正相だと+3dBのピークが出来るので、−6dB落ちクロスとして滑らかなつながりを求める、−6dB落ちは正相でうまくつながり易い云々、の記述があります。結果としてそうなる、というのと、電気回路としての原則の話は分けて説明してもらわないとこまります。
ネットワーク計算ワークシートの使い方 (例はこのページのちょっと上にあります)
ネットワークの理論を究めようとすると、ユニット自体のインピーダンス、位相特性・・・・・という立ち入った議論が必要になります。しかし一方では「スピーカー作ってみたい」、けれど、「コンデンサ、て何?」という方もきっといらっしゃると思います。長岡先生の本を読んだだけで自分で定数を決めるのは結構難しいのではないかと思います。
私が作ったのは、ユニットのインピーダンスを単純Rとおくだけのものですが、EXCELの使い方をよく知らない方でも比較的簡単に使えるという点ではよく出来ている方と思いましたので、公開することにしました。net_simu.xlsをダウンロードしてください。6dB/oct、12dB/oct及びその混用に対応しています。太枠の中に数字を入れればグラフがすぐ出来ます。とりあえずgainだけ見ていただく分には簡単に使えるのではないかと思います。
上3つがハイパス(ローカット)フィルタ用で、トゥイータのインピーダンス(公称値ということにしましょう)、直列に入るコンデンサの容量、12dB/octとする場合の、ユニットに並列になるコイルのインダクタンス、を入れるのですが、6dB/octとしてコイルを使わない計算をするには、インダクタンスの所に大きな数字を入れてください。10000で十分です。
次の3つがローパス(ハイカット)フィルタ用で、ウーファのインピーダンス、直列に入るコイルのインダクタンス、12dB/octとする場合の、ユニットに並列になるコンデンサの容量、を入れるのですが、6dB/octとしてコンデンサを使わない計算をするには、容量の所に0を入れてください。
一番下がタイムアライメント検討用で、2つのユニットから聴取位置までの距離が等しければ0、ウーファが遠くなる方を+、近くなる方を−として、cm単位で入れるのですが、目の毒ですからしばらくは0にしておくのをお勧めします。